机器学习-回归
(广义)线性回归是机器学习很基础也是很重要的内容,如何来更好地理解线性回归(linear regression)和逻辑回归(logistic regression)。
线性回归
高斯分布
最大似然估计
最小二乘本质
梯度下降法
评判标准(metric)
假设样本独立同分布(iid-independent and identically distributed),线性回归总是可以找到一个超平面使得样本点以一种“对称”的方式分布在该超平面两边。这样,样本点到超平面的距离(假设以此定义为误差)也是独立同分布的,并且是均值为0,方差为某定值的高斯分布(中心极限定理)。
中心极限定理意义:
实际问题中,很多随机现象可以看做众多因 素的独立影响的综合反应,往往近似服从正态分布。
- 城市耗电量:大量用户的耗电量总和
- 测量误差:许多观察不到的、微小误差的总和
- 注:应用前提是多个随机变量的和,有些问题 是乘性误差,则需要鉴别或者取对数后再使用这样就可以认为所有的预测值也满足一个高斯分布,就可以得到每个预测值的概率,那么所有预测值的联合概率分布(即为每个预测值边缘概率乘积因为iid)就是似然函数。
对似然函数取对数(即为高斯的对数似然),最大似然函数的最值求解过程就是一个最小二乘的过程: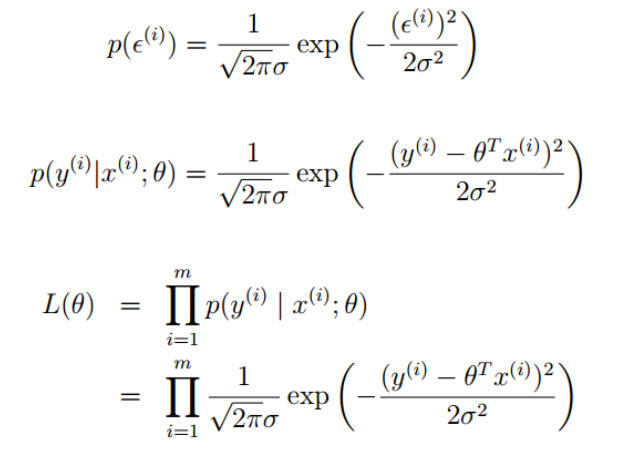
所以线性回归使用的最小二乘法(损失函数使用“二乘”距离)可以用最大似然估计来解释: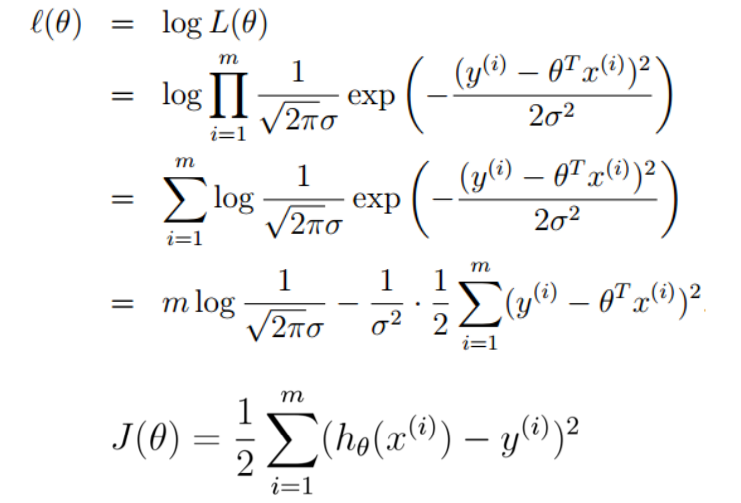
以“二乘”距离作为损失函数,一定可以取得最小值,因为损失函数展开后“二次项”为$\theta^T X^TX \theta$,系数$X^TX$为半正定的,所以损失函数一定为一个凸函数,必有极小值。求解损失函数的最小值,最值点必为驻点,驻点梯度必为零。
线性回归有解析解: $\theta=(X^TX)^{-1}X^Ty$,但是这种方法求解时间复杂度太高$O(n^3)$。一个有效的优化方案就是使用梯度下降法来计算,先初始化一个初值$\theta_0$,然后求解负梯度方向,进行迭代$\theta=\theta - \alpha \frac{\partial J(\theta)}{\partial \theta}$, $\alpha$为学习率。梯度下降算法使用时,不是拿所有样本计算梯度,也不是只拿一个样本计算梯度,而是随机地拿某几个(minibatch)计算梯度,并且将该梯度作为全局的梯度来进行下降,即所谓SGD(Stochastic Gradient Descent)。
参数复杂度惩罚因子: 为了防止过拟合,在损失函数中加上L1或者L2正则。线性回归中有特有称呼: Lasso回归(L1正则),Ridge回归(L2正则),Elastic Net(L1,L2正则结合)。
评估系数可以选择
$$
R^2 = 1 - RSS/TSS
$$
其中,
$$
RSS = \sum_{i=1}^{m}(y_i - \bar y)^2
$$
$$
TSS = \sum_{i=1}^{m}(\hat y - \bar y)^2
$$
$y_i$为样本值,$\bar y$为样本均值,$\hat y$为估计值。
$R^2$越大越好(注意,$R^2$可能为负)。
Logistic回归
分类问题的首选算法
logistic回归是一个广义线性模型,其中sigmoid函数就是某个随机变量(指数族分布)取值的概率。若在线性回归之后再取一个概率,那不就是一个分类问题了吗?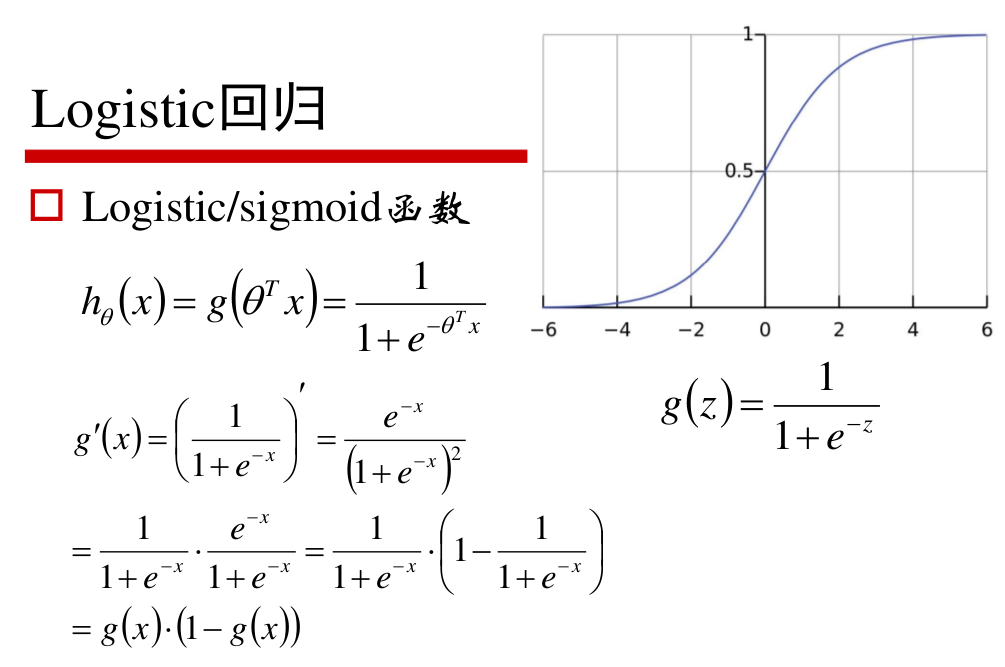
对数几率: 一个事件发生的概率比上不发生的概率称为几率,再取对数,称为对数几率。
logit函数: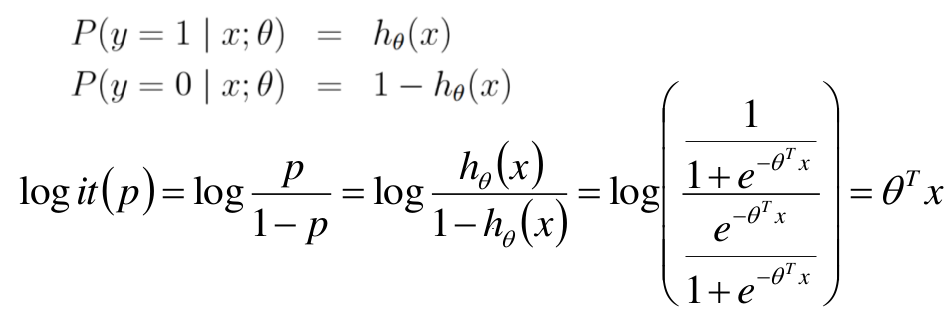
所以logistic回归是线性的,在取sigmoid函数之前得到的结果往往称呼为logits,原因就在此。
多分类: Softmax回归
目标函数
技术点
梯度下降算法
最大似然估计
特征选择
文中部分截图来源于 小象学院-邹博老师的机器学习课件(支持正版)